求二进制中1的个数

问题描述¶

任意给定一个32位无符号整数n，求n的二进制表示中1的个数。

普通法¶

原理：移位+计数

func BitCount(a uint32) (num uint32) {
	for num = 0; a != 0; a >>= 1 {
		fmt.Println(a, a&1)
		num += a & 1
	}
	return
}

缺点：这样会循环整个byte数组，运行较慢

快速法¶

原理：不断清除n的二进制表示中最右边的1，同时进行累加，直到n为0。

func BitCount(a uint32) (num uint32) {
	for num = 0; a != 0; num++ {
		a &= a - 1
	}
	return
}

优点：其运算次数与输入n的大小无关，只与n中1的个数有关。

查表法¶

动态建表¶

由于表示在程序运行时动态创建的，所以速度上肯定会慢一些，把这个版本放在这里，有两个原因

1. 介绍填表的方法，因为这个方法的确很巧妙。
2. 类型转换，这里使用移位的方式实现切分uint32变成[]byte

func BitCount1(a uint32) (num uint8) {
	//建表
	BitSetTable := [256]byte{0}
	//init
	for i := 0; i < 256; i++ {
		BitSetTable[i] = byte(i&1) + BitSetTable[i/2]
	}
	//拆分uint32为4个uint8的字段
	var b []byte
	b = append(b, byte(a>>24), byte(a>>16), byte(a>>8), byte(a))
	//查表
	num = BitSetTable[b[0]] + BitSetTable[b[1]] + BitSetTable[b[2]] + BitSetTable[b[3]]
	return
}

先说一下填表的原理，根据奇偶性来分析，对于任意一个正整数n

1. 如果它是偶数，那么n的二进制中1的个数与n/2中1的个数是相同的，比如4和2的二进制中都有一个1，6和3的二进制中都有两个1。为啥？因为n是由n/2左移一位而来，而移位并不会增加1的个数。

2. 如果n是奇数，那么n的二进制中1的个数是n/2中1的个数+1，比如7的二进制中有三个1，7/2 = 3的二进制中有两个1。为啥？因为当n是奇数时，n相当于n/2左移一位再加1。

再说一下查表的原理

对于任意一个32位无符号整数，将其分割为4部分，每部分8bit，对于这四个部分分别求出1的个数，再累加起来即可。而8bit对应种01组合方式，这也是为什么表的大小为256的原因。

所谓的 静态表-4bit和静态表-8bit就是在动态建表的基础之上，手动的给出动态建表过程中的表信息，从而实现相较于动态建表更快的时间复杂度。原理与动态建表一致。

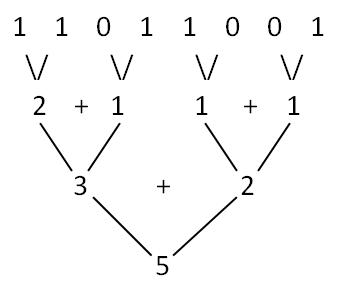
平行算法¶

func BitCount2(n uint32) uint32 {
	n = (n & 0x55555555) + ((n >> 1) & 0x55555555)
	n = (n & 0x33333333) + ((n >> 2) & 0x33333333)
	n = (n & 0x0f0f0f0f) + ((n >> 4) & 0x0f0f0f0f)
	n = (n & 0x00ff00ff) + ((n >> 8) & 0x00ff00ff)
	n = (n & 0x0000ffff) + ((n >> 16) & 0x0000ffff)
	return n
}

参考资料¶

1. 博客园，算法-求二进制数中1的个数 ，2010